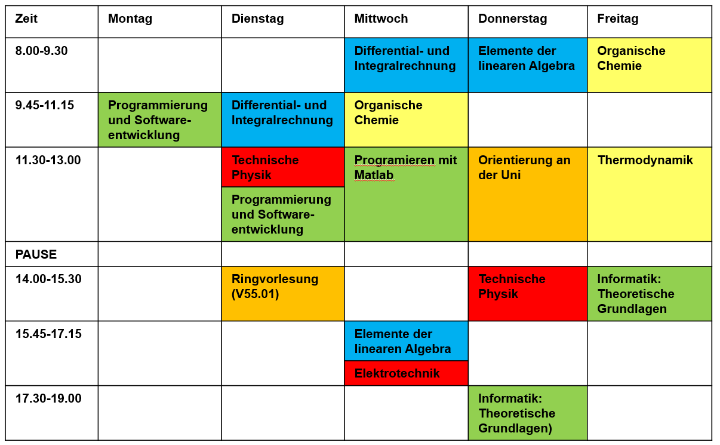
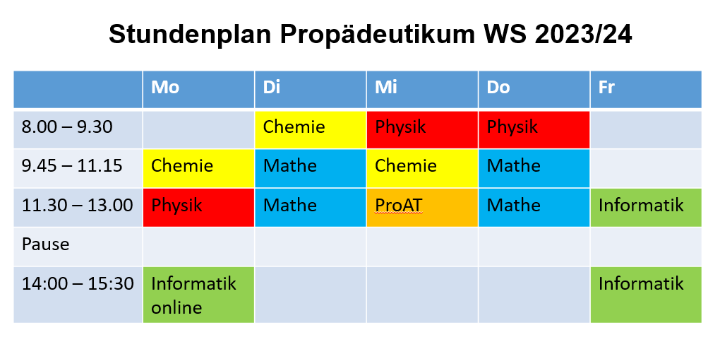
Der zweite Teil des zweisemestrigen Propädeutikums findet in Form der Vertiefungskurse im Sommersemester vom 8. April bis zum 19. Juli 2024 statt.
Wintersemester (Teil 1)
Umfang: 8 SWS (Semesterwochenstunden)
Dauer: ein Semester
Wann: Von November bis Ende Februar
Themenübersicht
In diesem Kurs werden Grundlagen der Mathematik vermittelt, die die Voraussetzung für das Verständnis höherer mathematischer Zusammenhänge bilden.
1. Brüche, Potenzen, Wurzeln und Logarithmen
2. Aussagen, Mengen und Zahlen
3. Gleichungen, Ungleichungen und Betragsgleichungen
4. Summenzeichen, Fakultät und Binomialkoeffizient
5. Vollständige Induktion
6. Abbildungen und Elementare Funktionen
7. Folgen, Grenzwerte und Stetigkeit
8. Differentialrechnung
9. Integralrechnung
10. Vektoren und Matrizen
Sommersemester (Teil 2)
Im Gegensatz zum Wintersemester setzt sich der zweite Teil des Kurses im Sommersemester voraussichtlich aus den folgenden zwei unabhängigen Vertiefungsmodulen zusammen, die einzeln oder kombiniert besucht werden können.
Wir beraten Sie gerne persönlich in der Wahl einer sinnvollen Kombination von Fächern beziehungsweise Modulen angepasst an das von Ihnen angestrebte Studienfach.
Vertiefungsmodul Differential- und Integralrechnung
Umfang: 4 SWS
Dauer: ein Semester
Wann: Von April bis Juli
Themenübersicht
1. Folgen, Grenzwerte und Stetigkeit
2. Differentialrechnung
3. Integralrechnung
Vertiefungsmodul Elemente der linearen Algebra
Umfang: 4 SWS
Dauer: ein Semester
Wann: Von April bis Juli
Themenübersicht
Dieser Kurs dient unter anderem als Vorbereitung für die Höhere Mathematik (insbesondere HM 1 für Ingenieurstudiengänge).
- Vektorräume
- Systeme linearer Gleichungen
- Lineare Abhängigkeit und lineare Unabhängigkeit
- Basen und Koordinatenvektoren
- Normen und Skalarprodukte
- Geraden und Ebenen
- Lineare Abbildungen und ihre Darstellungen
- Matrizenrechnung
- Basiswechsel
Kontakt und Beratung
MINT-Kolleg Baden-Württemberg
Azenbergstr. 12, 70174 Stuttgart, Carl-von-Bach-Haus. Telefonische Sprechstunden des Sekretariats: Mo, Di, Do und Fr von 9:00 bis 12:00 Uhr. Bitte halten Sie sich an die angegebenen Zeiten.

Barbara Schüpp-Niewa
Dr.Dozentin

Kateryna Serebryakova
Dr.Verwaltung. Telefonische Sprechstunde: Mo, Di, Do und Fr von 13:00 bis 17:00 Uhr und Mi von 9:00 bis 17:00 Uhr.